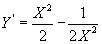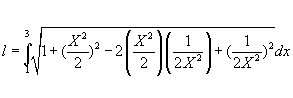Tabla de Integrales

Integral por partes

Es una integral por partes, se resuelve por medio de la formula

Si (a) y (s) son constantes, tenemos; 

Sustituyendo

La integral del lado derecho de la expresión es otra integral por partes, resolviendo;

Sustituyendo tenemos;

La integral de lado derecho de esta última expresión es igual a la integral de lado izquierdo, transponiendo términos tenemos;

 

Sumando ambas integrales

Eliminando el coeficiente de la integral y transponiendo al lado derecho:

Solución:

Entradas Interesantes

Biografías de Matemáticos

Completación de cuadrados

Solución a la ecuación de segundo grado            

Matemáticas y la vida

Sistema de numeración Indoarábigo

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.

Propiedades de la integral definida

 Si f(x) y g(x) son dos funciones continuas en el intervalo de integración [a,b] y k una constante cualquiera:

     

a)    Si los límites que integración coinciden, la integral definida vale cero.

b)   El valor de la integral definida cambia de signo si se permutan los límites de integración.

c)  La integral del producto de una constante por una función es igual a la constante por la integral de la función.

d)    La integral definida de una suma de funciones es igual a la suma de integrales (Propiedad de linealidad)·

  

e)     Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].

Entradas Interesantes

Biografías de Matemáticos

Completación de cuadrados

Solución a la ecuación de segundo grado            

Matemáticas y la vida

Sistema de numeración Indoarábigo

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.

Volumen de sólidos por integración triple

Utilizar una integral triple para hallar el volumen del sólido mostrado en las siguientes figuras:

solo me dan estos dos puntos.

z=4-x^2

y=4-x^2

cuando

x≥0

y≥0

z≥0

y la otra es:

z= 9-x^2

y= -x+2

cuando

x≥0

y≥0

z≥0

2) Respuesta

1) Respuesta

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.

Integral, cambio de variable

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.

Longitud de arco.

Determinar la longitud del arco de la curva desde el punto x=1 hasta el punto x=3.

Solución:

La derivada es:

Sustituyendo;

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.