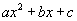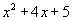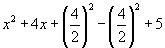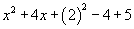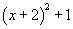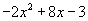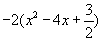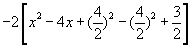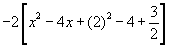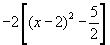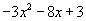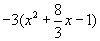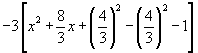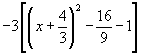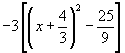La siguiente expresión es una ecuación de 2do grado, siempre y cuando el coeficiente a≠0.
La mayoría de las personas utilizamos la famosa resolvente de la ecuación de 2do grado, es decir:

para obtener así las raíces o también llamadas soluciones. Pero muchos aceptamos esta resolvente como un dogma y pocos nos preocupamos por investigar de donde sale esa expresión que garantiza la solución a la ecuación de segundo grado. Para los curiosos y los que no lo son voy a resolverles y explicarle los pasos para llegar a la resolvente de segundo grado.
1) Vamos aplicar la técnica de completación de cuadrados, es necesario saberla de lo contrario se te hará un poco difícil entender los pasos siguientes, para comprenderla puedes visitar mi blog en el siguiente enlace: http://linaresgsj.blogspot.com/2011/02/completacion-de-cuadrados.html
2)

como sabemos que a≠0, podemos pasarlo al segundo miembro dividiendo y se anulara, la expresión queda de la siguiente manera:
3) Si aplicamos la técnica de completación de cuadrados, debemos darnos cuenta que debemos proceder de la siguiente manera:
a) Se selecciona el valor absoluto del término central, es decir, aunque este término sea negativo siempre lo tomaras positivo.
b) Divides este término por 2 y a esa expresión la elevas al cuadrado.
En nuestro caso sería:

c) Suma y resta este nuevo término a la expresión dada.
4) Después de aplicar estos pasos anteriores debes obtener la siguiente expresión
d) A los tres primeros términos se le completa cuadrado, a los dos últimos se le realizan operaciones.
5) Si realizamos el paso d) debe quedar:
6) Transponiendo términos al segundo miembro queda:
7) Resolviendo el segundo miembro por la técnica de mínimo común denominador se obtiene:

8) Extrayendo raíz cuadrada a ambos miembros queda:

9) Simplificando la raíz y aplicando propiedades de radicacion, es decir:


11) Transponiendo términos al primer miembro, queda:

12) Finalmente, aplicamos la suma de fracciones con igual denominador y recordamos que la raiz cuadrada arroja dos posibles resultados, uno positivo y otro negativo, en conclusión aquí les muestro la resolvente de la ecuación de 2do grado.
Entradas
Interesantes
Si
consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un
comentario. Gracias.