La parábola

Una parábola es el lugar geométrico de un punto que se mueve en un plano de tal manera que su distancia de una recta fija, situada en el plano , es siempre igual a su distancia de un punto fijo del plano y que no pertenece a la recta. El punto fijo se llama foco y la recta fija directriz de la parábola. La definición excluye el caso en que el foco está sobre la directriz.

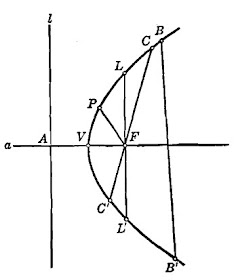
Designemos por F y 1 (ver figura), el foco y la directriz de una parábola, respectivamente. La recta “a” que pasa por F y es perpendicular a 1 se llama eje de la parábola. Sea A el punto de intersección del eje y la directriz. El punto V, punto medio del segmento AF, está, por definición, sobre la parábola; este punto se llama vértice. El segmento de recta, tal como BB’, que une dos puntos cualesquiera diferentes de la parábola se llama cuerda; en particular, una cuerda que pasa por el foco como CC’, se llama cuerda focal. La cuerda focal LL’ perpendicular al eje se llama lado recto. Si P es un punto cualquiera de la parábola, la recta FP que une el foco F con el punto P se llama radio focal de P, o radio vector.

Lehmann, C. (1999). Geometría analítica. México: Limusa-Noriega Editores

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.

Solución a la ecuación de segundo grado

La siguiente expresión es una ecuación de 2do grado, siempre y cuando el coeficiente a≠0.

La mayoría de las personas utilizamos la famosa resolvente de la ecuación de 2do grado, es decir:

para obtener así las raíces o también llamadas soluciones. Pero muchos aceptamos esta resolvente como un dogma y pocos nos preocupamos por investigar de donde sale esa expresión que garantiza la solución a la ecuación de segundo grado. Para los curiosos y los que no lo son voy a resolverles y explicarle los pasos para llegar a la resolvente de segundo grado.

1) Vamos aplicar la técnica de completación de cuadrados, es necesario saberla de lo contrario se te hará un poco difícil entender los pasos siguientes, para comprenderla puedes visitar mi blog en el siguiente enlace: http://linaresgsj.blogspot.com/2011/02/completacion-de-cuadrados.html

2)

como sabemos que a≠0, podemos pasarlo al segundo miembro dividiendo y se anulara, la expresión queda de la siguiente manera:

3) Si aplicamos la técnica de completación de cuadrados, debemos darnos cuenta que debemos proceder de la siguiente manera:

a) Se selecciona el valor absoluto del término central, es decir, aunque este término sea negativo siempre lo tomaras positivo.

b) Divides este término por 2 y a esa expresión la elevas al cuadrado.

En nuestro caso sería:

c) Suma y resta este nuevo término a la expresión dada.

4) Después de aplicar estos pasos anteriores debes obtener la siguiente expresión

d) A los tres primeros términos se le completa cuadrado, a los dos últimos se le realizan operaciones.

5) Si realizamos el paso d) debe quedar:

6) Transponiendo términos al segundo miembro queda:

7) Resolviendo el segundo miembro por la técnica de mínimo común denominador se obtiene:

8) Extrayendo raíz cuadrada a ambos miembros queda:

9) Simplificando la raíz y aplicando propiedades de radicacion, es decir:

10) La raiz cuadrada de la siguiente expresion es

11) Transponiendo términos al primer miembro, queda:

12) Finalmente, aplicamos la suma de fracciones con igual denominador y recordamos que la raiz cuadrada arroja dos posibles resultados, uno positivo y otro negativo, en conclusión aquí les muestro la resolvente de la ecuación de 2do grado.

Entradas Interesantes

Biografías de Matemáticos

Completación de cuadrados

Solución a la ecuación de segundo grado            

Matemáticas y la vida

Sistema de numeración Indoarábigo

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.

¿Qué es la matemática?

No es fácil definir lo que se entiende por matemáticas. Si acudimos al diccionario de la real academia española encontramos: “Matemática es la ciencia que trata de la cantidad”. A su vez, cantidad es todo lo que es capaz de aumento y disminución y puede, por consiguiente, medirse o enumerarse. Finalmente, “ciencia” es “el conocimiento cierto de las cosas por sus principios y sus causas”. Todas son definiciones imprecisas, de las que difícilmente, quien no tenga ya una idea previamente formada, podrá deducir algo concreto sobre lo que realmente es la matemática. Sin embargo, por costumbre que data de siglos y de acuerdo con la opinión de las personas que en cada momento de la historia se han considerado los conductores de las matemáticas y sus mas visibles exponentes , todos tenemos o creemos tener una idea de lo que queremos decir cuando nos referimos a la matemática. Por lo menos en los aspectos que podríamos llamar “interiores” al dominio de la matemática, esta idea es clara e indiscutida, si bien al acercarnos al contorno o las fronteras con otras ramas del conocimiento, nos encontramos con terrenos cuya rotulación como “matemática” ya no es tan indiscutible ni tan compartida, paradójicamente, la matemática, que trabaja siempre con definiciones bien precisas y con entes perfectamente delimitados, al tratarse de sí misma, en su totalidad, no parece que admita una definición exacta, ni que tenga limites bien determinados.

Tal vez esta imprecisión derive de su dualidad entre ciencia natural, que persigue encontrar y entender las leyes de la naturaleza, y filosofía o arte, en el sentido mas puro y platónico de estas disciplinas. Practica, o hace matemática, quien a partir de unos datos numéricos “calcula” un área o un volumen o el tiempo necesario para que un proyectil alcance su meta. Pero también hace y practica matemática quien busca propiedades de los números primos, establece teoremas sobre figuras geométricas o aclara la equivalencia entre postulados básicos de la teoría de conjuntos.

Aparentemente, esta dualidad de la matemática, podría pensarse como una consecuencia de su extención y que, por lo tanto, sus distintos aspectos son partes alejadas de un mismo cuerpo original, cada día mas distanciadas entre sí. Pero no es este el caso. El distanciamiento y poca conexión entre sus partes son solo aparentes. La unidad de la matemática es indisoluble y poco se puede avanzar en una dirección si se pierden de vista las otras ramas hermanas. Las aplicaciones son el estimulo y muchas veces la guía de la matemática pura. Pero sin esta, la matemática aplicada se agota rápidamente y se convierte en poco tiempo en cúmulo de recetas rutinarias, sin perspectiva de progreso.

Santaló, Luis A. et al. Enfoques: hacia una didáctica humanista de las matemáticas. (1994) “¿Qué es la matemática?”. Buenos Aires, Editorial Troquel. (pp 21-24). Párrafo 1,2 y 3.

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.

Volumen de sólidos por integración triple

Utilizar una integral triple para hallar el volumen del sólido mostrado en las siguientes figuras:

solo me dan estos dos puntos.

z=4-x^2

y=4-x^2

cuando

x≥0

y≥0

z≥0

y la otra es:

z= 9-x^2

y= -x+2

cuando

x≥0

y≥0

z≥0

2) Respuesta

1) Respuesta

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.

límite trigonométrico indeterminado

Integral, cambio de variable

Si consideras que este artículo ha aclarado tus dudas, te invitamos a dejar un comentario. Gracias.